Sharing helps us build more free tools
Spearman's Rank Correlation Coefficient measures the correlation between two ordinal variables.
Ordinal variables are ordered values, for example, someone's placing in a race. The difference between two people's placing in the race does not tell you how far one person was in front of the other. That would require both people's time to complete the race.
When To Use Spearman Correlation
The Spearman Correlation Calculator is useful when you want to see the correlation between two ordinal variables.
The Pearson correlation coefficient calculator is useful if you want to calculate the correlation between two continuous variables.
What Does the Spearman's Rank Correlation Coefficient Mean?
The Spearman Rank Correlation Coefficient can be between -1 and 1.
A negative correlation coefficient means that two variables are negatively correlated. When one variable changes the other changes in the opposite direction. For example, when one variable increases, the other variable decreases.
A spearman's correlation coefficient of -1 is a perfect negative correlation.
A positive correlation coefficient means that two variables are positively correlated. When one variable changes then the other changes in the same direction. For example, when one variable increases, the other variable increases as well.
A spearman's rank correlation coefficient of 1 is a perfect positive correlation.
A correlation coefficient close to zero means that the two variables are not correlated. Changes in one variable do not correlate with changes in the other variable.
How To Calculate Spearman Correlation
Upload your data using the input
Click the input box at the top of the page and select your dataset
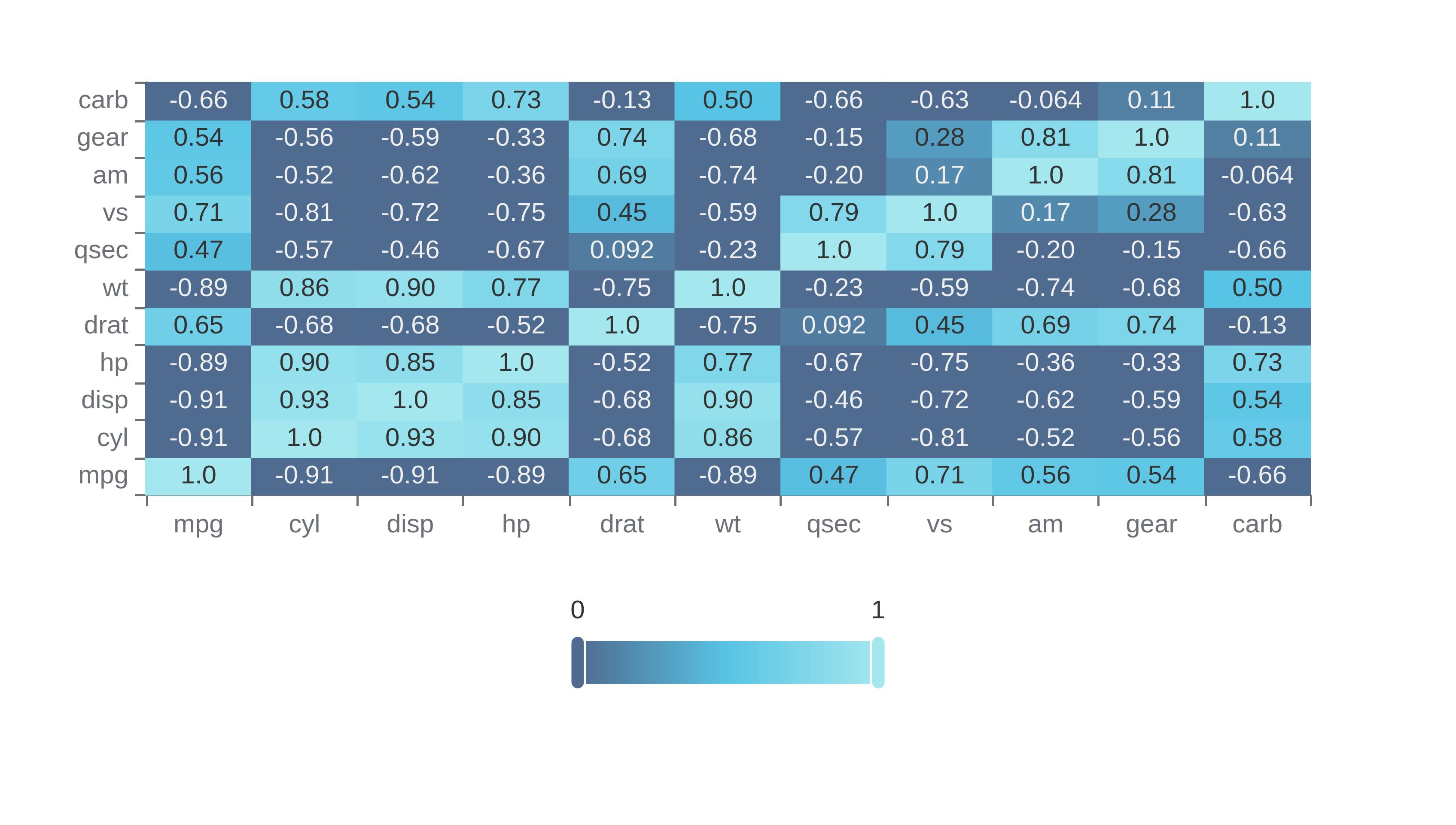
View and analyse your correlations
See what columns correlation with other columns the most
Download your correlations
Click the download button on the chart to download a png of your correlations
Spearman's Correlation Coefficient Formula
The Spearman rank correlation can be calculated with the following formula:
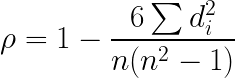
Rho is Pearson's rank correlation coefficient
d_i is the difference between the two ranks of each data point
n is the number of data points